FraktallarGiriş

Doğada çevremize bakarken, aşağıdaki gibi karmaşık bitkileri fark etmiş olabilirsiniz:

Bir Eğreltiotu, ana dalından aynı şekilde çıkan birçok küçük yaprakdan oluşur.

Bu Romanesco brokoli, daha büyük olanın etrafında dönen küçük oluşur.

Başlangıçta, bunlar son derece karmaşık şekiller gibi görünür - ancak daha yakından baktığınızda, her ikisinin de nispeten basit bir desen izlediğini fark edebilirsiniz: bitkilerin her bir birimi bitkinin bütününe benzer, sadece daha küçüklerdir. Aynı desen daha küçük ölçeklerde tekrar tekrar yenilenir.

Matematikte, bu özelliğe kendine benzerlik diyoruz ve buna sahip şekillere fraktallar denir. Fraktallar, tüm matematiğin en güzel ve en tuhaf nesnelerinden bazılarıdır.

Kendi fraktallarımızı oluşturmak için basit bir desenle işe başlayıp daha sonra daha küçük ölçeklerde tekrar tekrar yenileyerek devam etmeliyiz.

En basit örüntülerden biri bir ucundan iki doğru parçası dahaçıkan bir doğru parçasıdır. Bu örüntüyü tekrarlarsak, bu mavi segmentlerin her ikisinin de uçlarından iki dal daha çıkacaktır.

Tüm dalların uzunluğunu ve açısını değiştirmek için mavi noktaları hareket ettirebilirsiniz. Ardından, aşağıdaki çubuğu](->#fern-slider) kaydırarak {yin} tekrarlanma sayısını artırın.

Dalların konumuna bağlı olarak, yukarıdaki , veya gibi görünen tamamen farklı desenleri oluşturabilirsiniz. Başka hangi şekilleri oluşturabilirsiniz?

Bir başka ünlü fraktal da Sierpinski üçgenidir. Burda ise, büyük, eşkenar bir üçgenle başlayıp, sonra kalan parçalardan tekrar tekrar küçük üçgenler kesiyoruz.

Son şeklin bütününün üç özdeş birimden](target:x) nasıl oluştuğuna ve bunların her birinin, tüm üçgenin, daha da küçük kopyalarından oluştuğuna dikkat edin! Üçgeni sonsuza dek büyütmeye devam ettiğinizde, desenler ve şekillerin her zaman tekrarlanmaya devam ettiğini görürsünüz.

Bu bölümün başında gördüğümüz bitkiler fraktallar 'a benziyorlar, ancak gerçek hayatta hakiki fraktal oluşturmak mümkün değildir. Aynı modeli tekrar tekrar, daha küçük ve daha küçük tekrarlarsak bile, sonunda bölünemeyecek olan hücrelere, moleküllere veya atomlara ulaşırdık.

Ancak, matematik sayesinde gerçek fraktalların “sahip olacağı” özellikleri düşünebiliriz - ve bunlar çok çok şaşırtıcı…

Fraktalların Boyutları

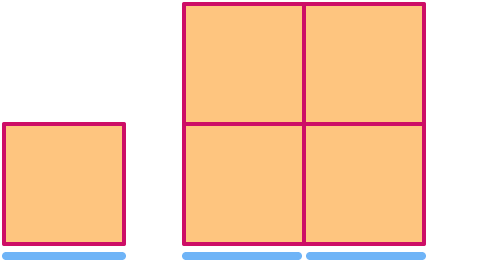
İlk olarak, fraktalların boyutlarını düşünelim. Bir doğru parçasının boyutu dir. Tahmin edilebileceği gibi, onu 2 kat büyüttüğümüzde uzunluğu 21=2 kat artar.

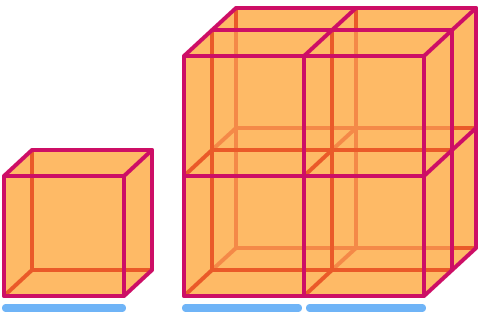
Bir kare boyuta sahiptir. 2 kat büyüttüğümüzde, alanı 22= kat artar.

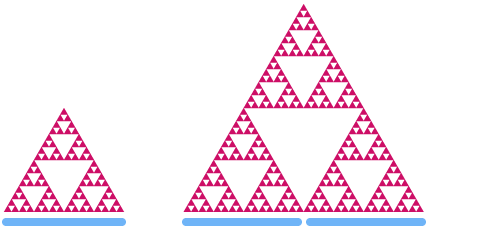
Bir küpün boyutu vardır. onu, 2 kat büyütürken, hacmi 23= kat artmaktadır. Görüntüdeki büyük küp, daha küçük olanın 8 kopyasından oluşur!

Şimdi ise Sierpinski üçgenine bakalım. Bu üçgeni 2 katına çıkarırsak, "alan" ın kat arttığını görebilirsiniz.

Diyelim ki d, Sierpinski üçgeninin boyutu. Yukarıdaki ile aynı modeli kullanarak 2d=3 elde ederiz. Başka bir deyişle, d = ≈ 1.585…

Ama durun… bir şeyin tamsayı olmayan bir boyutu nasıl olabilir? İmkansız görünüyor, ama bu fraktalların garip özelliklerinden sadece biri. Aslında, fraktallara isimlerini veren de budur: Fraktalların, kesirli bir boyutu vardır.

Her yinelemede, Sierpinski üçgeninin bazı bölgelerini yok ediyoruz. Bunu sonsuza kadar birçok kez yapabilseydik, aslında herhangi bir yüzeyi kalmazdı: bu yüzden Sierpinski üçgeni 2 boyutlu bir yüzey ile 1 boyutlu bir çizgi arasında bir şeydir.

Birçok fraktal kendine benzer olmakla birlikte, daha iyi bir tanım fraktalların tamsayı olmayan bir boyuta sahip olan şekiller, olduğudur.

Koch Kar Tanesi

Doğada fraktallara benzeyen birçok şekil var. Bu bölümün başında, zaten bazı bitkiler görmüştük. Diğer harika örnekler, kar taneleri ve buz kristalleridir:

Kendi fraktal kar tanemizi oluşturmak için, tekrar tekrar uygulayabileceğimiz basit bir prosedür bulmak zorundayız.

Sierpinski üçgeni gibi, tek bir eşkenar üçgenle başlayalım. Bununla birlikte, her adımda _daha küçük üçgenleri silmek yerine, kenar boyunca ekleyelim. Her yeni, küçük üçgenin kenar uzunluğu, önceki adımdaki üçgenlerin 'dır.

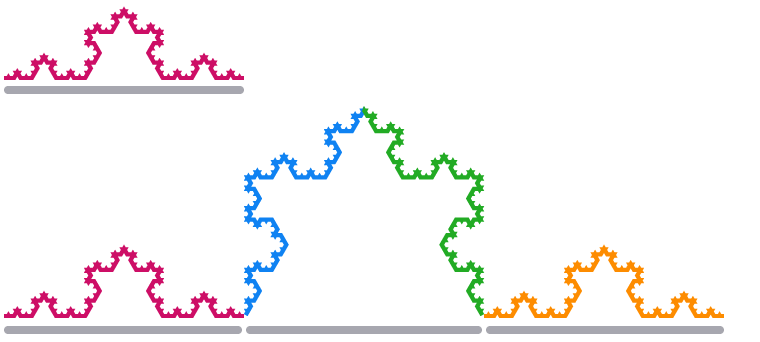
Ortaya çıkan şekle, İsveçli matematikçi Helge von Koch adını taşıyan Koch kar tanesi denir. Bir kez daha, kar tanesinin kenarlarındaki her bir küçük bölümün, şeklin bütünü ile tamamen aynı göründüğüne dikkat edin.

Koch Kar Tanesi'nin bir kenarını 3 katı büyüttüğümüzde, uzunluğu .

Yukarıdaki boyutlar ve büyüme ölçekleri arasındaki aynı ilişkiyi kullanarak, denklemini alıyoruz. Bu da, Koch Kar Tanesi'nin boyutunun d=log34≈1.262 olduğu anlamına gelir.

Alan

Koch kar taneleri oluşturmak neredeyse yinelemeli bir dizi gibidir: başlangıç şeklini (bir üçgen) biliyoruz ve bir terimden diğerine nasıl geçileceğini biliyoruz (her kenara daha fazla üçgen ekleyerek):

yeni üçgen

İlk adımdan sonra, eklenen yeni üçgenlerin sayısı her adımda kat artmaktadır. Aynı zamanda, bu yeni üçgenlerin alanı, her adımda da bir azalmaktadır.

Diyelim ki ilk üçgenin 1 birim alanı var. sonraki üç üçgenin toplam alanı 3×19=13 olur. Aşağıdaki adımların tümü, ortak oranı olan , oluşturur.

Sonsuz geometrik seri toplamını hesaplamak için gereken formülü kullanarak, Koch kar tanesinin, toplam alanını bulabiliriz.

A=1+13×1=85=1.6.

Çevre

Koch kar tanesinin, çevresini de hesaplamaya çalışabiliriz. Daha önce gördüğümüz gibi, çevre uzunluğu her adımda katına çıkar.

Bu, bir kez daha geometrik bir serimiz olduğu anlamına gelir - ancak bu durumda çevra, [[>>>>,|0'a yaklaşır|dilk terimi yoktur] 'herhangi bir sayoya yaklaşmaz. Bu, Koch kar tanesi çevresinin aslında sonsuz uzunluğunda olduğu anlamına gelir!

Bu mantıksız görünüyorsa, çevreyi her adımda 43 ile çarptığımızı ve bunu sonsuza kadar defalarca yaptığımızı unutmayın.

Aynı anda sonlu alanı ve sonsuz çevresi olan bir şekil neredeyse düşünülemez - ancak bu, fraktalların beklenmedik birçok özelliğinden sadece biridir.

Kendi fraktallarınızı yaratmanın başka yollarını bulabilir misiniz?

“Ruhum her yerdeki donmuş fraktallara geziniyor…”

Menger Süngeri

Fraktalların, yukarıdaki örneklerde olduğu gibi hep "düzlemsel" olmaları gerekmez. 3 boyutlu olan en ünlü fraktallardan biri, ilk olarak 1926'da matematikçi Karl Menger tarafından bulunan Menger süngeri' dir.

Tek bir küple başlıyoruz ve her bir yüzüne tekrar tekrar daha küçük ve daha küçük delikler açıyoruz. Her yeni adımda oluşan kübik delik, önceki deliğin genişliğinin 'ü kadardır.

Normalde, (3x3x3) bir küp (347}) 27 küçük küpten oluşur, ancak şekilde gördüğüniz gibi bunlardan bazılarını sildik. Dolayısı ile Menger süngeri, kendisinden 3 kat daha küçük olan kopyasından oluşur.

Şimdi, yukarıdaki Koch kar tanesi için yaptığımız gibi Menger süngerinin de d boyutunu hesaplamaya çalışabiliriz. Bu durumda 3d=20 veya d=log320≈2.727 alırız.

Sonsuza kadar delik açmaya devam ettiğimizi varsayarsak, aslında geriye bir hacim kalmaz. Bu yüzden bu küp “tam olarak” 3 boyutlu değildir!

Fraktal Sahil Şeritleri

Şimdiye kadar gördüğümüz tüm fraktalların temel özelliklerinden biri, sonsuza dek “yakınlaştırabilmemiz” ve her zaman aynı örüntüleri bulabilmenizdir. 1920 yılı dolaylarında, İngiliz matematikçi Lewis Fry Richardson, bunun birçok ülkenin sınırı veya sahil şeridi için geçerli olduğunu fark etti.

Ülkenin temel şekli ile başlayıp, yakınlaştırdıkça nehir girişleri, koylar ve körfezleri ekleyip, ardından her bir sahili, kayaları, çakıl taşlarını eklemek gibi

Bir ülkenin sınırının uzunluğunu hesaplamaya çalışırken - ne kadar yakınlaştıracağınıza ve hangi köşe ve girinti ve çıkıntıları dahil edeceğinize karar vermek, önemli bir sorundur.

Britanya'nın kıyı şeridinin uzunluğunu ölçmenin yollarından biri, uzun bir cetvel almak, plajlarında dolaşmak ve sonra tüm mesafeleri toplamaktır.

Cetvel ${rulers[index]} km uzunluğundaysa, onu ${count} kez kullanmalıyız, bu yüzden toplam sahil şeridimiz ${count} × ${rulers[index]} = ${count * rulers[index]} km olur.

Daha küçük ve daha küçük cetvellerle bu işe devam edebiliriz, kıyı şeridinin uzunluğuna ilişkin sonuç her seferinde biraz daha uzun olur. Tıpkı daha önce Koch Kar tanesinde olduğu gibi, İngiltere'nin sahil şeridi sonsuza kadar uzuyormuş gibi gözüküyor! Buna genellikle kıyı şeridi paradoksu denir.

On yıllar sonra, matematikçi Benoit Mandelbrot, IBM’de çalışırken Richardson’ın atılan bir kütüphane kitabındaki çalışmalarına rastladı. Kitabın önemini ve fraktallar ile boyutlar hakkında yapılan yeni araştırmalarla nasıl ilişkili olduğunu hemen fark etti.

Britanya'nın kıyı şeridi kesinlikle fraktal "görünüyor", ancak daha önce gördüğümüz diğer fraktallar gibi kendine benzer değil. Boyutunu bulmak için, kareli bir kağıda çizebilir ve kesiştiği kare sayısını sayabiliriz.

Başlangıçta 88 kesişen kare vardır. Kıyı şeridini 2 kat büyütürsek, 197 kesişen kare olur - iki katından fazla!

Kıyı şeridinin boyutu 19788 kat arttı. Daha önce olduğu gibi, bu sahil şeridinin boyutu

d=log219788≈1.16

Bunu daha büyük karelerle tekrarlarsak, İngiltere sahil şeridinin boyutunun aslında yaklaşık 1.21 olduğunu görürüz. Mandelbrot, bu fraktal boyutun aynı zamanda bir şeklin pürüzlülüğünün bir ölçüsü olduğunu fark etti - bu yeni kavram ile, matematik ve bilimin diğer birçok alanında önemli uygulamalar buldu.

Doğa ve Teknolojiden Daha Fazla Fraktal

Gerçek fraktallar hiçbir zaman doğada görünmezken, fraktallara neredeyse benzeyen birçok nesne vardır. Zaten bitkiler, kar taneleri ve sahil şeritlerini görmüştük ve işte size birkaç örnek daha:

Orta Asya'daki dağ silsilesi

Hindistan'da Ganj Nehri Deltası

Yıldırımlar

Retinadaki kan damarları

ABD'deki Büyük Kanyon

Bulutlar

Tüm bu nesneler, tamamen rastgele oluşmuş gibi görünebilir, ancak tıpkı fraktallar gibi, bunların nasıl oluştuğunu belirleyen bir örüntü vardır. Matematik, şekilleri daha iyi anlamamıza yardımcı olabilir ve fraktalların tıp, biyoloji, jeoloji ve meteoroloji gibi alanlarda uygulamaları vardır.

Bilgisayar tarafından oluşturulan fraktal şeklinde yeryüzü

Fraktalları, video oyunlarında veya bilgisayar tarafından oluşturulan filmlerde kullanılan manzaralar ve dokular gibi gerçekçi doğa “kopyaları” oluşturmak için de kullanabiliriz. Bu görüntüdeki su, dağlar ve bulutlar tamamen bir bilgisayar tarafından, fraktalların yardımıyla yapıldı!

Ayrıca, dijital görüntüleri sıkıştırmak, dosya boyutlarını azaltmak için bu işlemi tam tersine de çevirebiliriz. Bu konuyla ilgili ilk algoritmalar 1980'lerde Michael Barnsley ve Alan Sloan tarafından geliştirildi ve bugün hala yeni algoritmalar araştırılıyor.

Dili değiştir

Mathigon'da oturum açın

Paylaş

İlerlemeyi Sıfırla

Sözlük