FraktallarMandelbrot Seti

Önceki bölümlerde gördüğümüz tüm fraktallar yineleme adımları kullanılarak oluşturulur: belirli bir desenle başlayıp sonra tekrar tekrar yinelersiniz.

Bu, matematikte daha önce gördüğünüz başka bir konsepte benzer: rekursif seriler, belirli bir sayıyla başlarsınız ve daha sonra, bir sonraki sayıya ulaşmak için, aynı formülü tekrar tekrar uygularsınız.

Örnek olarak xn=xn−12 formülünü ele alalım ve terimlerini sayı doğrusu üzerinde gösterelim. x0 değerini değiştirebilirsiniz:

Sonuç dizisinin x0 başlangıç değerine bağlı olarak nasıl çok farklı davranabileceğine dikkat edin:

Şimdiye kadar yeni bir şey öğrenmedik. Ancak, yaklaşık bir asır önce, matematikçiler gerçek sayı doğrusu yerine karmaşık sayıları kullanınca bu dizilere ne olduğunu keşfetmeye başladılar. Keşifleri, tüm matematikteki en şaşırtıcı ve güzel sonuçlardan biri oldu.

Julia Setleri

Öncekiyle aynı diziyi kullanalım, xn=xn−12, ancak karmaşık düzlemde. Aşağıdaki koşullarda ne olduğunu görmek için x0 konumunu hareket ettirebilirsiniz. Seri yakınsayacak gibi görünüyorsa da, düzlemde karşılık gelen her noktayı mavi ile renklendirdiğimizde:

Gördüğünüz gibi, dizi x0 birim çember içinde olduğu sürece| birim çember dışında| x-ekseni üstünde]]| outside the unit square|above the x-axis]] (1 birim yarıçapına sahip çember) içinde kaldığı sürece dizi yakınsar.

Şimdi işleri biraz daha zorlaştıralım. Önceki sayının sadece karesini almak yerine, her seferinde sabit bir c sayısı ekleyelim (c herhangi bir karmaşık sayı olabilir). Başka bir deyişle, xn=xn−12+c. Sizce hala bir yakınsama döngüsü elde edebilir miyiz? Başka hangi şekilleri görebileceğimizi tahmin edebilir misiniz? Devam

Bu şemada, x0 konumunu ve c değerini değiştirebilirsiniz:

Sayılarda renklendirmeyle oluşan bu farklı şekillere Julia Sets denir. 1918 civarında iki Fransız matematikçi Gaston Julia ve Pierre Fatou tarafından birbirlerinden bağımsız olarak keşfedildi.

O zamanlar, Julia Kümelerinin gerçekte neye benzediğini görselleştirmeye yardımcı olacak bilgisayarlar yoktu. Julia ve Fatou gibi matematikçiler onlar hakkında sadece matematiksel olarak akıl yürütebildiler ve ancak nasıl göründüklerine dair kaba, elle çizilmiş eskizler gördüler.

Bugün böyle bir sorunumuz yok - aşağıdaki resimlerin hepsi farklı Julia setlerine ait. Farklı renkler, bu noktalardaki dizinin ne kadar çabuk saptığını gösterir:

Devam

Mandelbrot Seti

Farklı Julia setlerini oluştururken, her dizinin ıraksadığı ve tüm karmaşık düzlemin beyaz kaldığı bazı c değerleri olduğunu fark etmiş olabilirsiniz. Julia ve Fatou'dan birkaç on yıl sonra, yeni nesil matematikçiler bu beyaz alanların nasıl göründüğünü anlamaya çalıştı.

Önceki örnekte, c için sabit bir değer seçtik ve sonra düzlemi renklendirmek için x0 konumunu değiştirdik. Şimdi x0=0 değerini sabitleyelim ve bunun yerine c değerini değiştirelim.

Bir kez daha, dizilerin sınırlı kaldığı bölgeyi ortaya çıkarmak için karmaşık düzlem üzerinde boyayın. Hangi şekillerin görünmesini bekliyorsunuz?

xn=xn−12+${complex(c)}

x0=${complex(x0)}

x1=${complex(x1)}

x2=${complex(x2)}

x3=${complex(x3)}

…Bounded!Diverges!

Bu fraktal, Mandelbrot Seti olarak adlandırılır ve 90 ° döndürüldüğünde, neredeyse kafa, gövde ve iki kolu olan bir insana benzer. İlk kez 1978'de matematikçiler Robert Brooks ve Peter Matelski tarafından bir araştırma makalesinde tanımlanmış ve çizilmiştir:

Birkaç yıl sonra, Benoit Mandelbrot, daha sonra onun adını alan fraktal hakkında çok daha ayrıntılı bir görselleştirme oluşturmak için IBM'deki güçlü bilgisayarları kullandı. İlk çıktılar beklediğinden farklı görünüyordu - yazıcılarda çalışan teknisyenlerin, toz parçacıklarından veya yazıcı hatalarından kaynaklandığını ve fraktalların tanımlayıcı bir özelliği olmadığını varsayarak, kenarındaki “bulanıklığı” temizlediğini anlayana kadar ! Devam

Tüm fraktallar gibi Mandelbrot setini sonsuza dek “yakınlaştırabiliriz” ve her ölçekte yeni desenler bulabiliriz. Burada Mandelbrot setinin Denizatı vadisi olarak adlandırılan bir parçasını yakınlaştırabilirsiniz. Siyah noktalar, dizinin sınırlı olduğu Mandelbrot kümesinin_ içinde _yer almaktadır. Renkli noktalar, dizinin ıraksadığı [Mandelbrot kümesinin _dışındadır ve farklı renkler ne kadar hızlı sonsuzluğa gittiğini_gösterir:

Scale: ${pow(scale)}

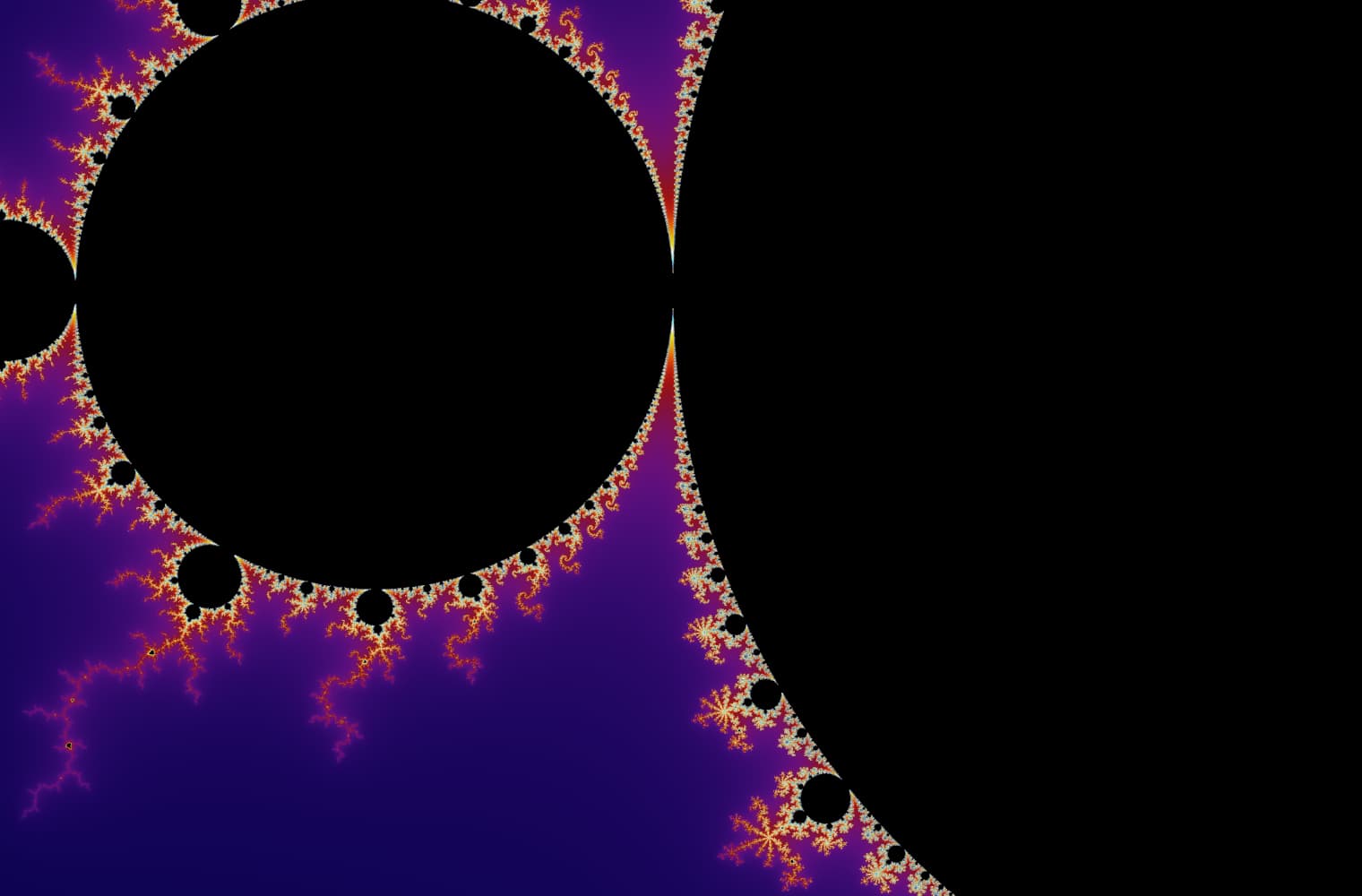
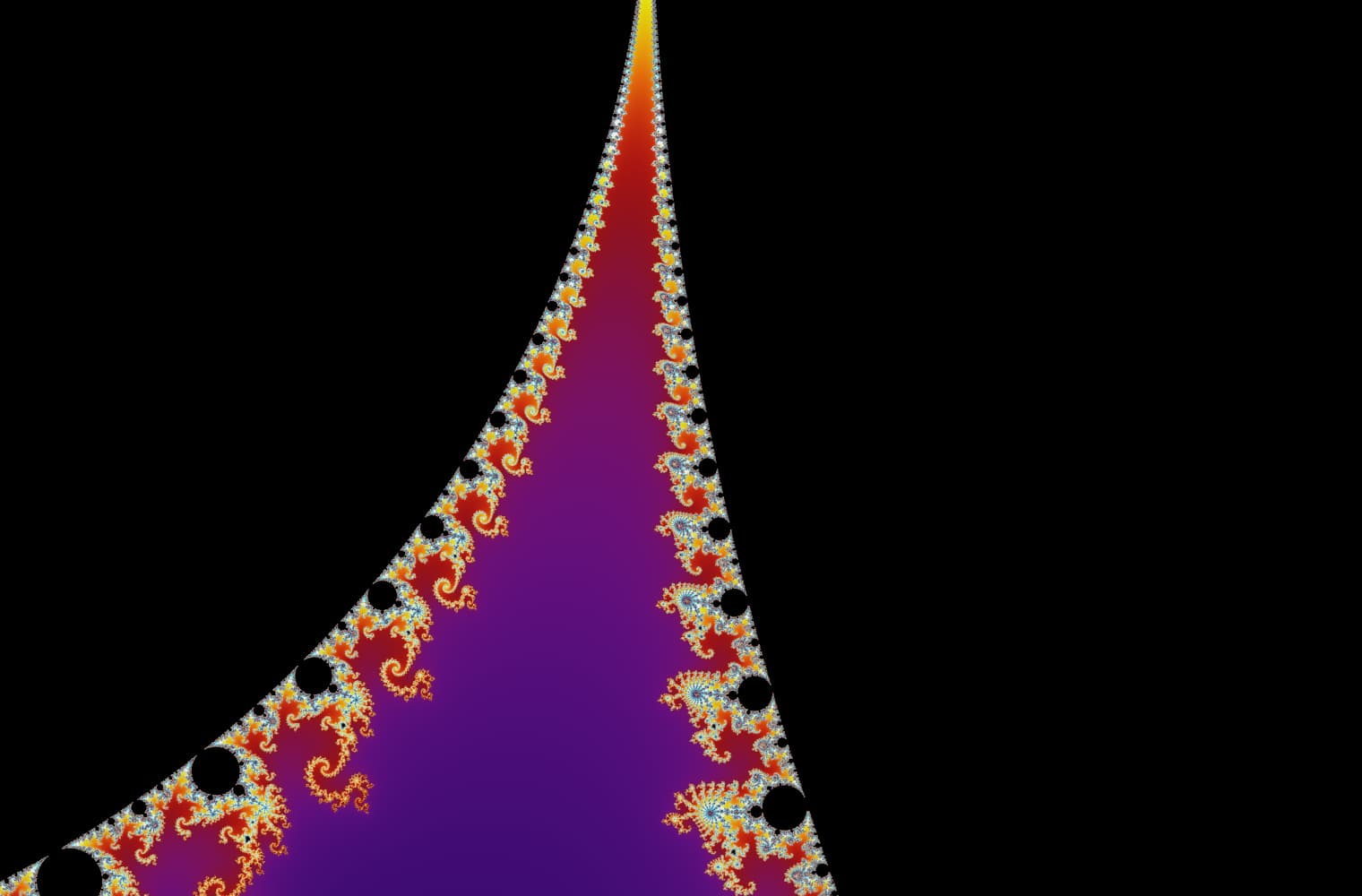
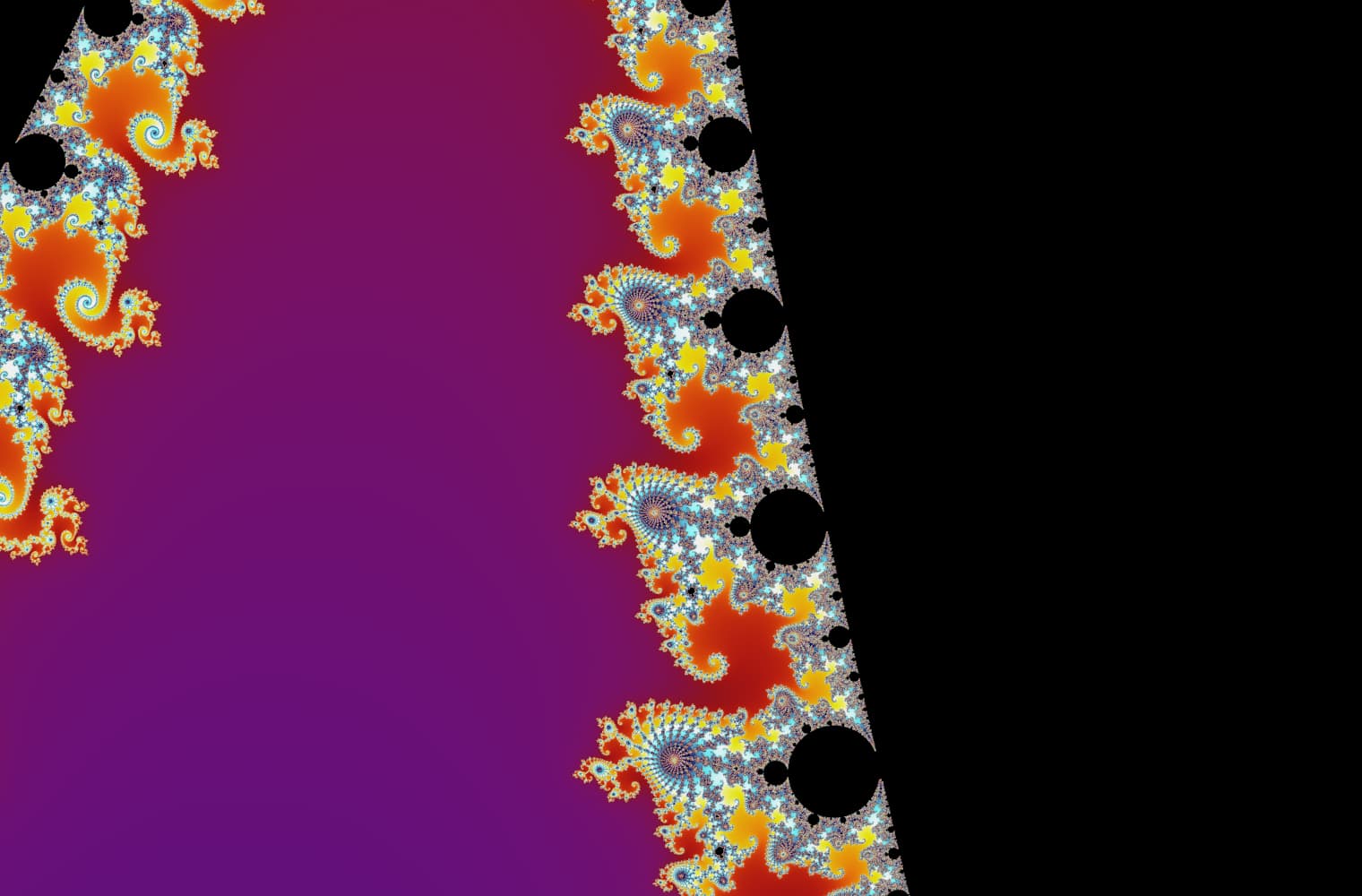
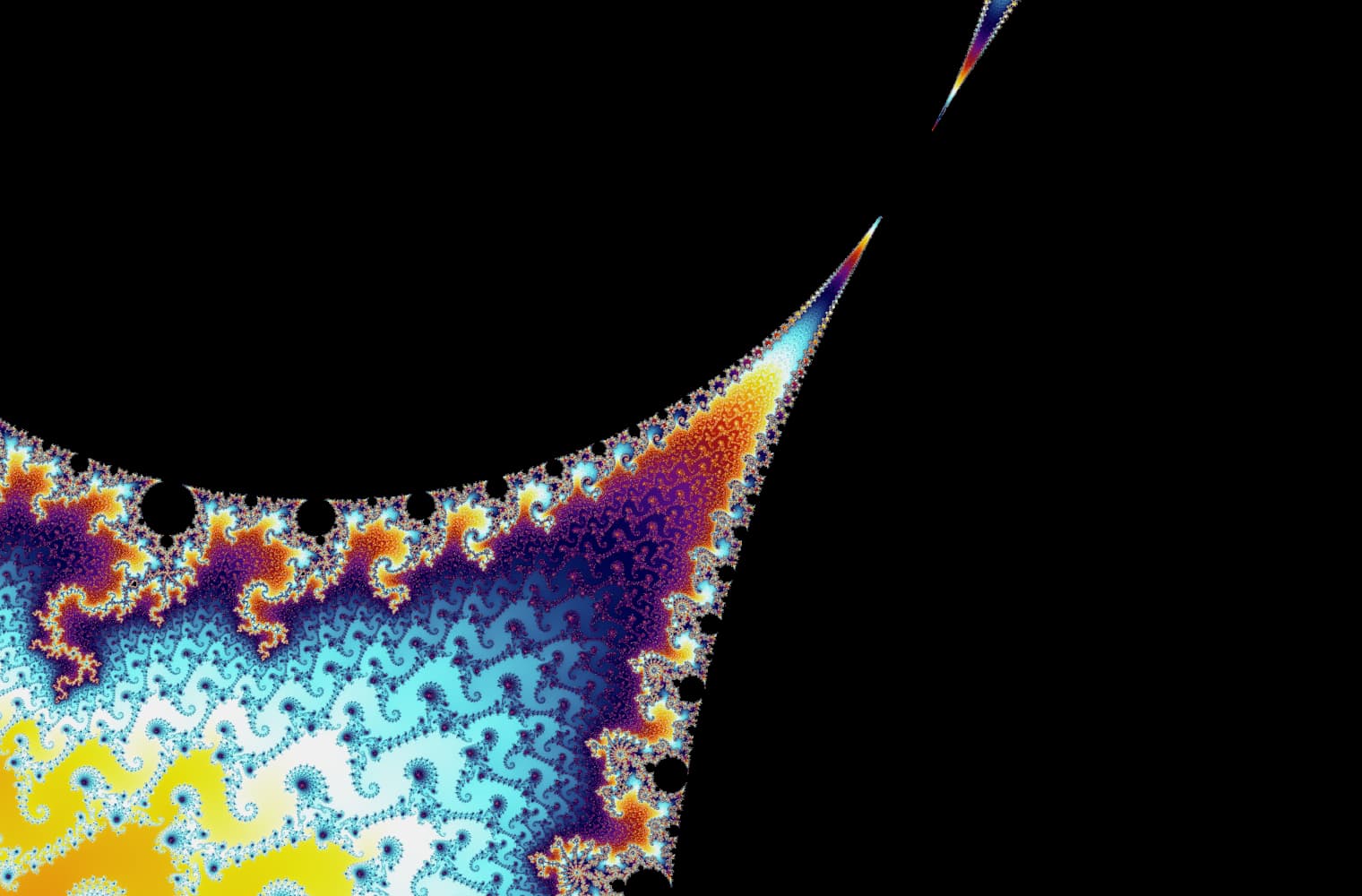
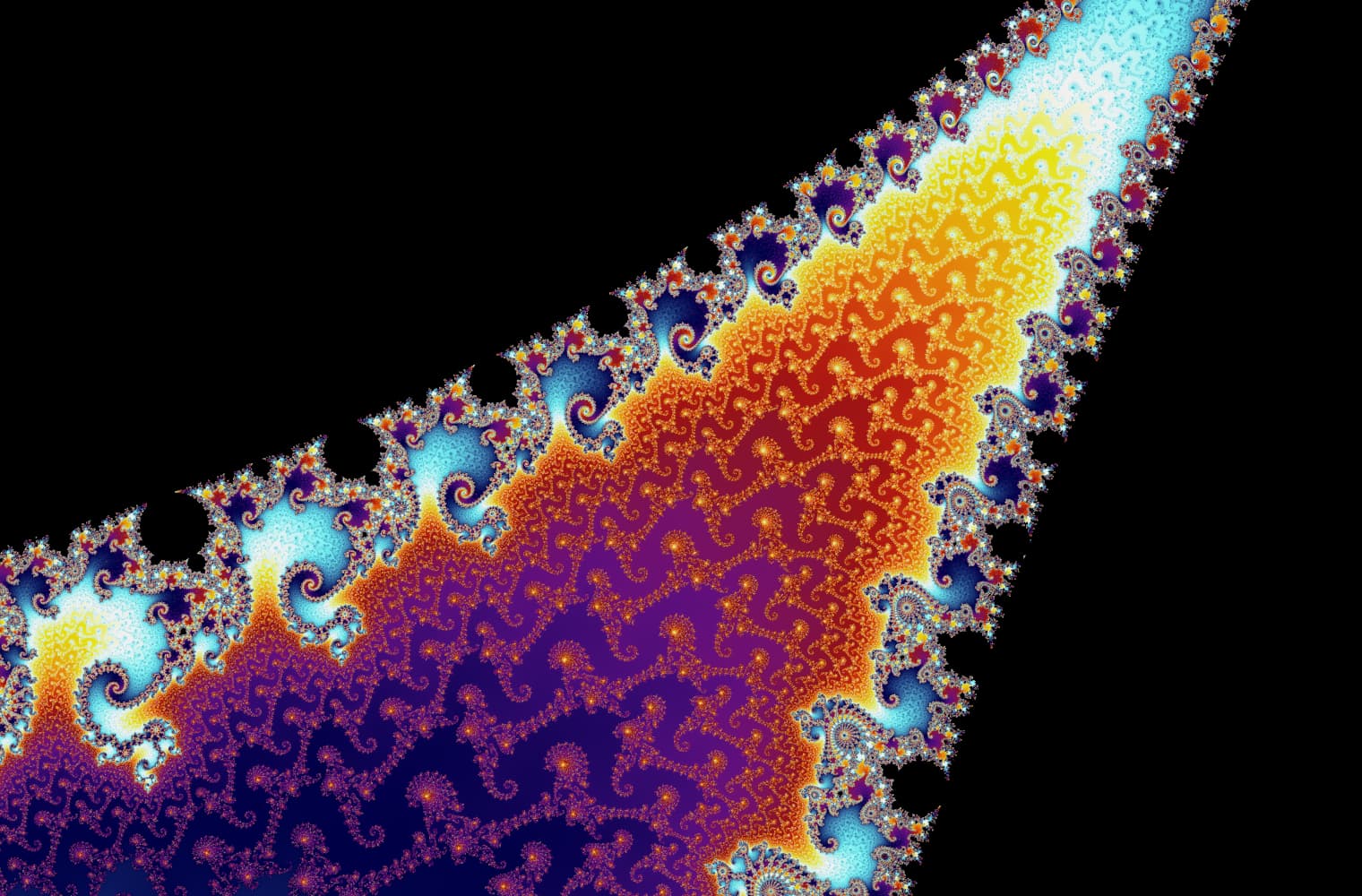
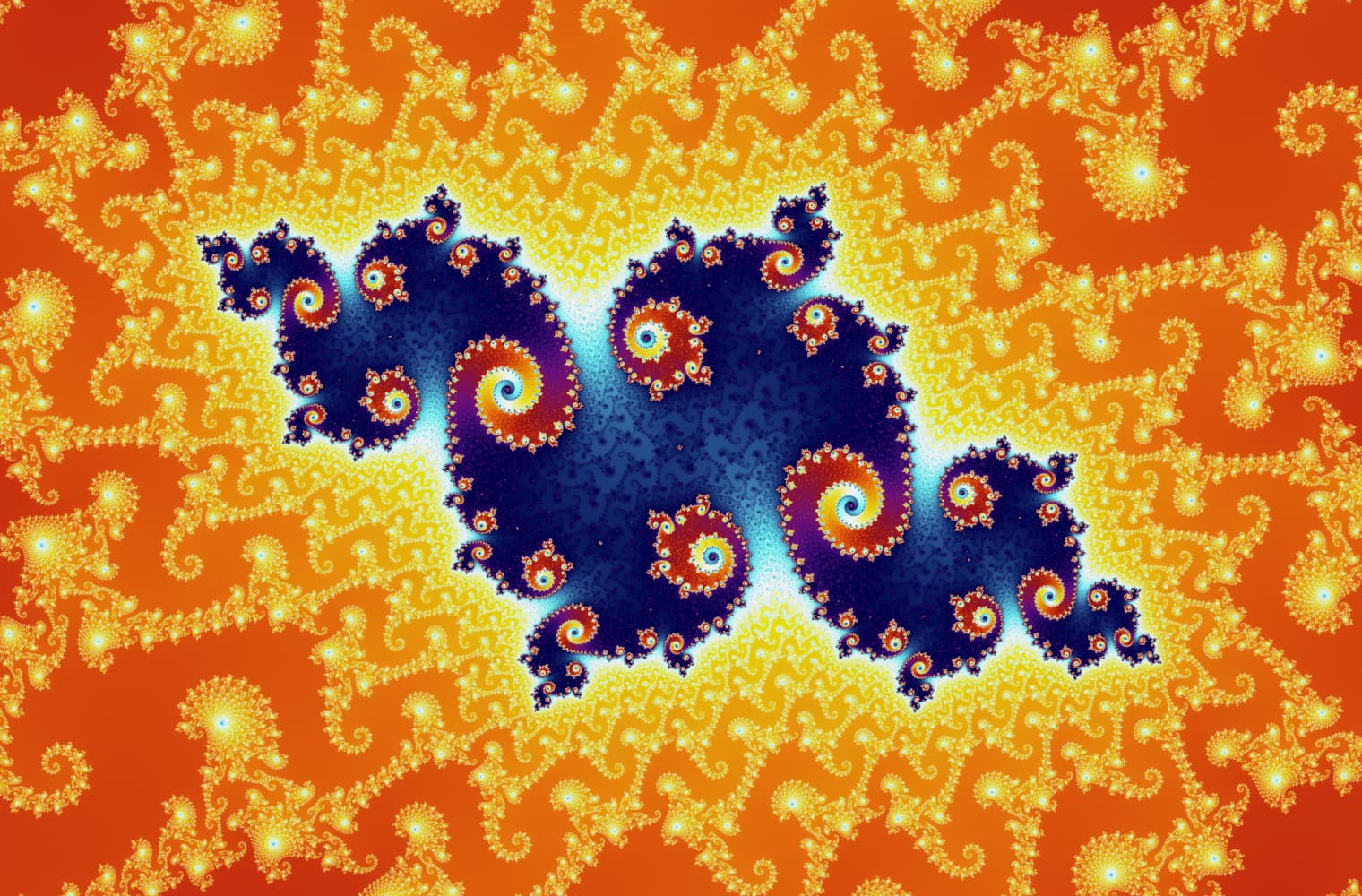
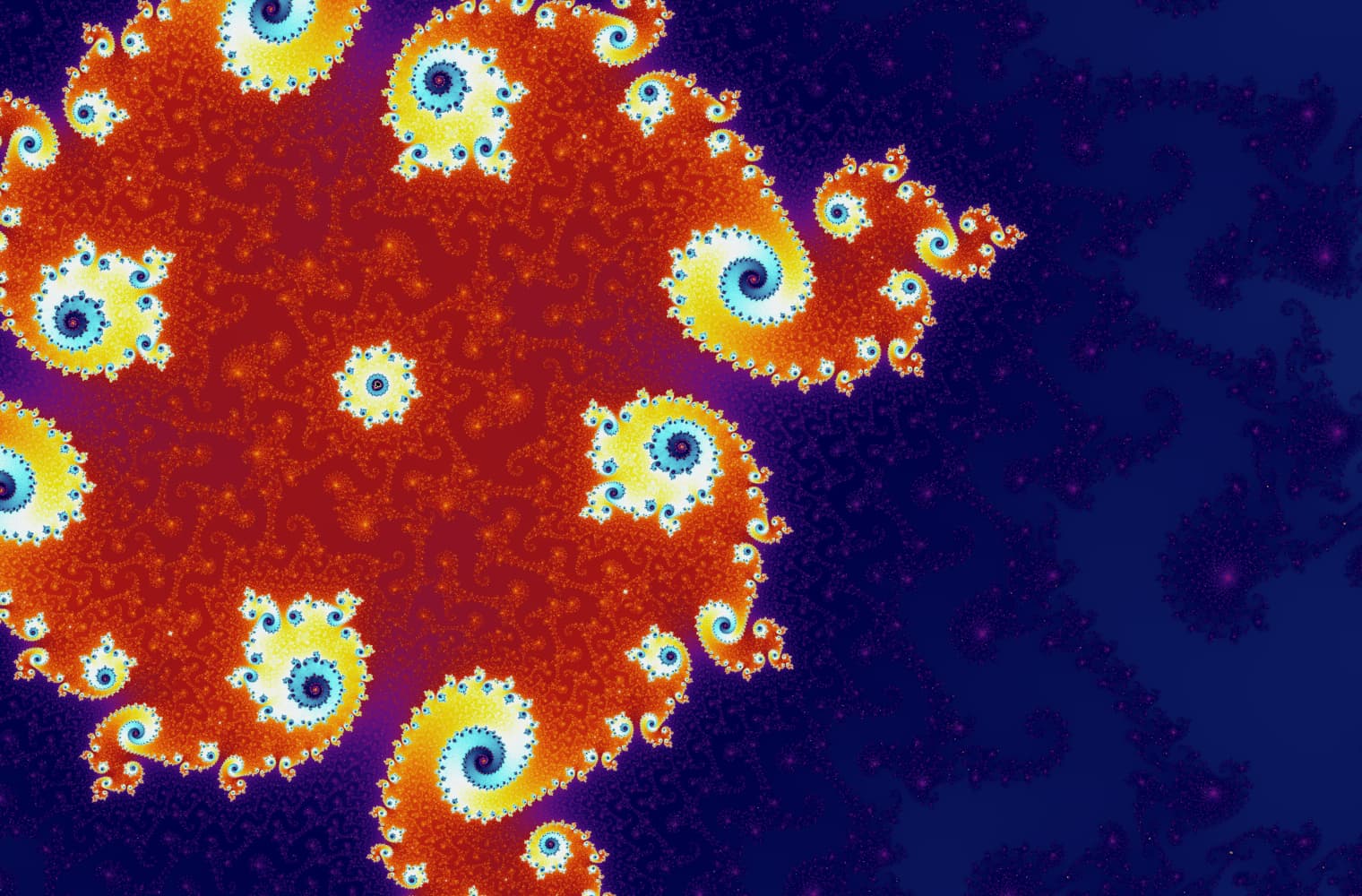
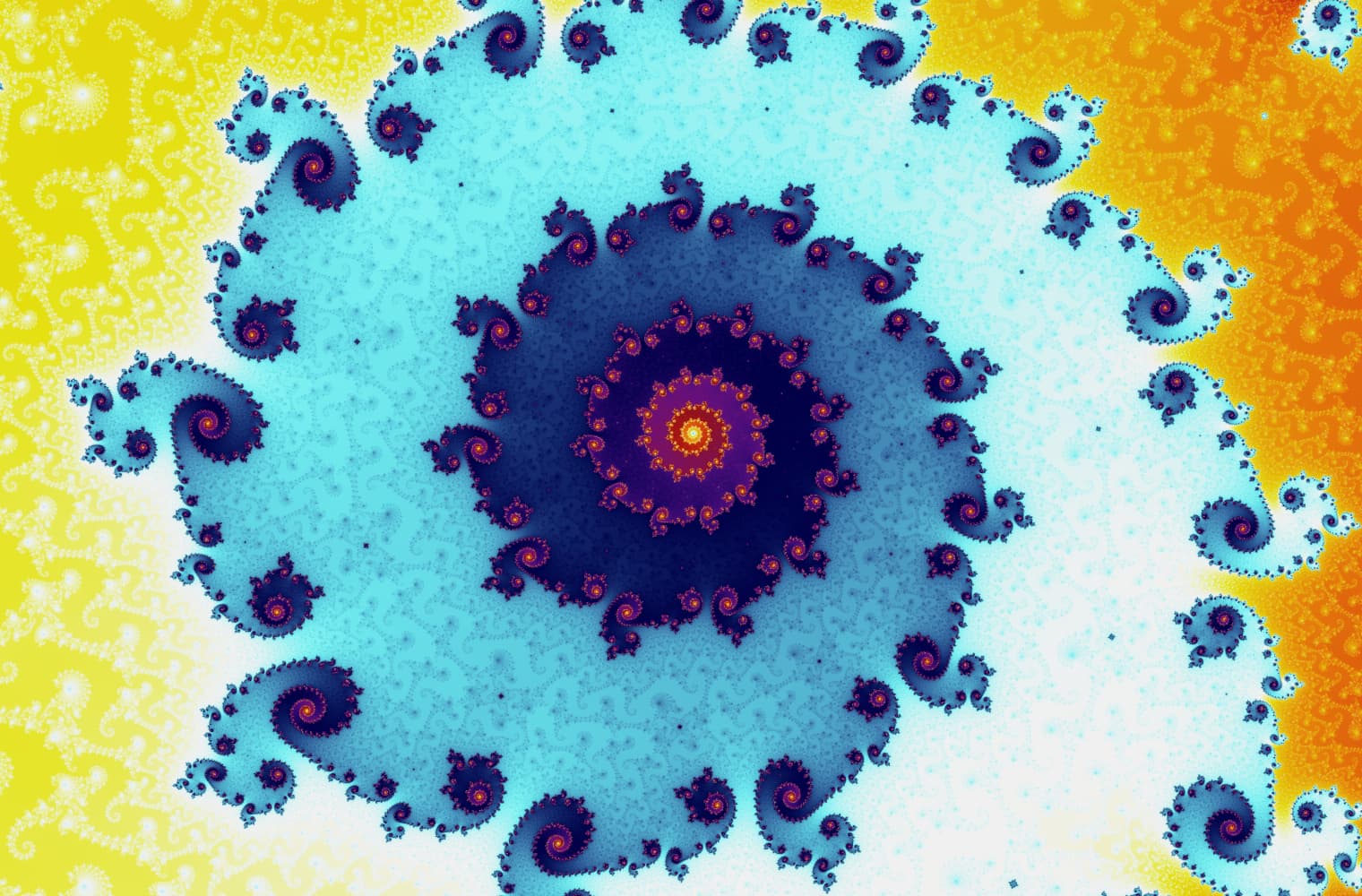
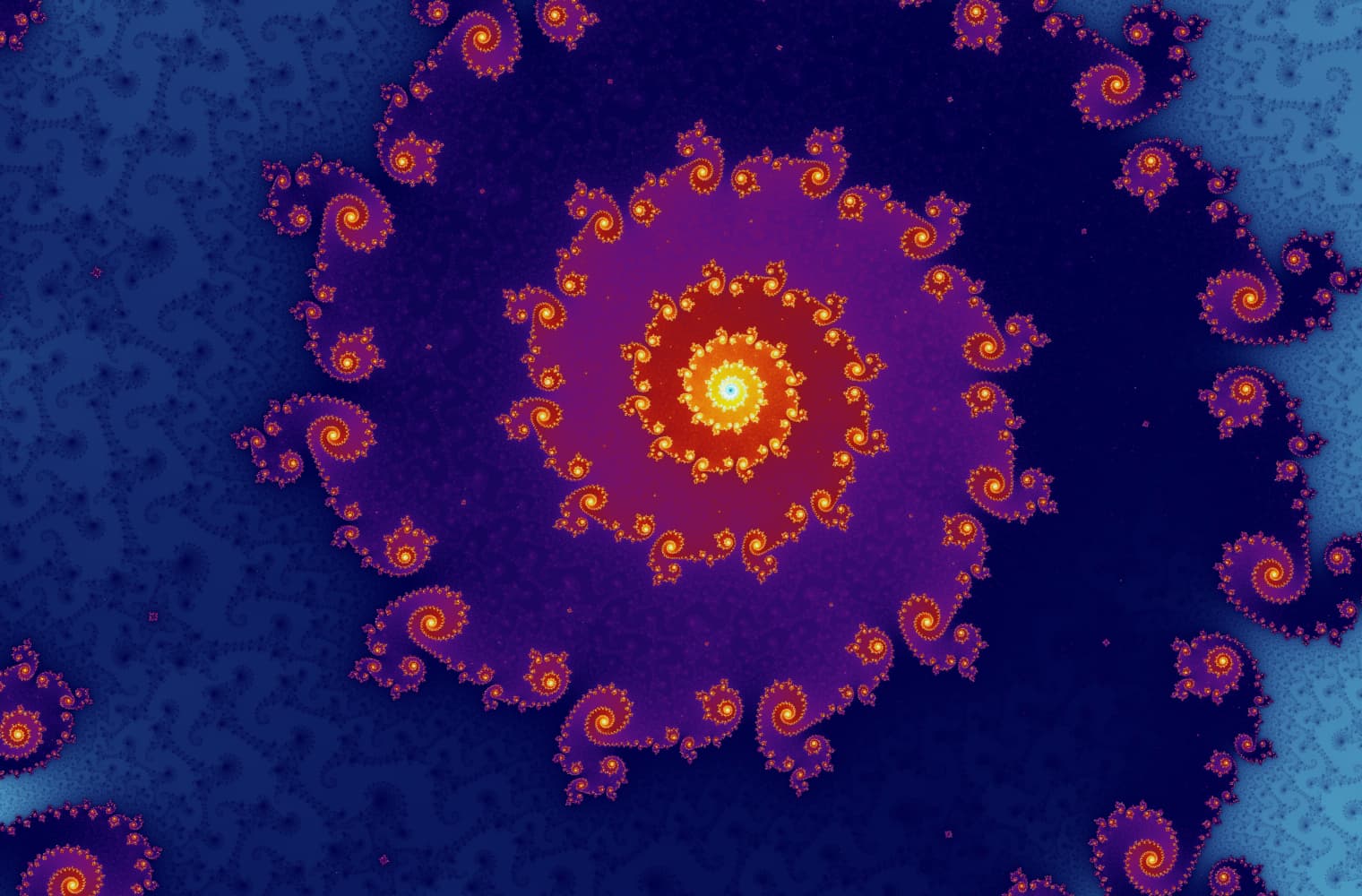
Bu kaydırma çizgisini kullanarak, 27 ayrı resimden oluşan bu seride 14 katrilyonu veya 254aşan yakınlaştırma düzeyine ulaşabilirsiniz. Modern bir dizüstü bilgisayar kullanarak bu resimleri oluşturmak yaklaşık 45 dakika sürdü. Mandelbrot seti sadece tek bir basit denklemle oluşturulabilir xn=xn−12+c, ancak sonsuz karmaşıklıkta ve şaşırtıcı derecede güzeldir.

c değerini Mandelbrot setinin etrafında hareket ettirdikçe, ilginç bir özellik fark edebilirsiniz:

• Mandelbrot setinin [ana gövdesi içerisindeki tüm dizilerıraksaryörüngeye ulaşır tek bir noktaya yakınsar.
• Üstteki büyük ampul içindeki diziler, noktadan oluşan yörüngesine ulaşıryakınsarıraksar .
• Küçük ampulün içindeki diziler uzunluğunda yörüngelere sahiptir.

Her ampul farklı boyutta bir yörüngeye sahiptir, daha küçük ampuller yörüngelerinde daha fazla noktaya sahiptir. Bu yörüngelerin büyüklüğü, Kaos teorisinde önemli bir kavram olan Lojistik Harita ile yakından ilişkilidir.