Üçgenler ve TrigonometriÜçgenlerin Özellikleri

Basitten başlayalım: üçgen, üç kenarı (kenarlar doğru parçası’dır), üç köşesi (kenarların birleştiği noktalar) olan kapalı bir şekildir. Aynı zamanda toplamları derece olan üç iç açısı vardır.

Açıların büyüklüklerine göre üçgenleri sınıflandırabiliriz:

Bir __dik açılı üçgen__in yalnız bir dik açısı vardır.

Bir __geniş açılı üçgen__in yalnız bir geniş açısı vardır.

Bir __dar açılı üçgen__in dar açısı vardır.

Kolay lık olsun diye üçgenleri genelde benzer şekillerde işaretleriz. Köşeler ilk üç büyük harf A, B ve C, kenarlar ilk üç küçük harf a, b ve c ve açılar Yunan harfleri α, β ve γ (“alpha”, “beta” ve “gamma”) ile işaretlenirler.

A köşesinin karşısındaki kenar a, A köşesindeki açı α ile işaretlenir. Aynı işaretlendirme B/b/β ve C/c/γ için de geçerlidir.

Medyanlar

Kenarlarının orta noktaları işaretlenmiş bir üçgen görüyorsunuz.

Bir üçgende bir köşe ile karşısındaki orta noktayı birbirlerine bağlayan doğru parçasına medyan denir. Bu üçgenin üç medyanını da çizin. Üçgenin köşelerini hareket ettirince ne oluyor?

Öyle görünüyor ki medyanlar hep . Bu noktaya ağırlık merkezi diyoruz.

Medyanlar birbirlerini her zaman 2:1 oranıyla keserler. Üç medyan için de köşeden ağırlık merkezine olan uzaklık ağırlık merkezinden orta noktaya olan uzaklığın hep

Bir kartona bir üçgen çizin, kesip çıkarın ve üç medyanı da bulun. Eğer düzgün kesip medyanları da düzgün çizerseniz ağırlık merkezine bir kalem koyduğunuzda üçgeni bu kalemin üzerinde dengeli bir şekilde taşıyabilirsiniz ya da tam ağırlık merkezine yapıştırdığınız bir iple odanızın tavanına yere tam paralel olacak şekilde asabilirsiniz.

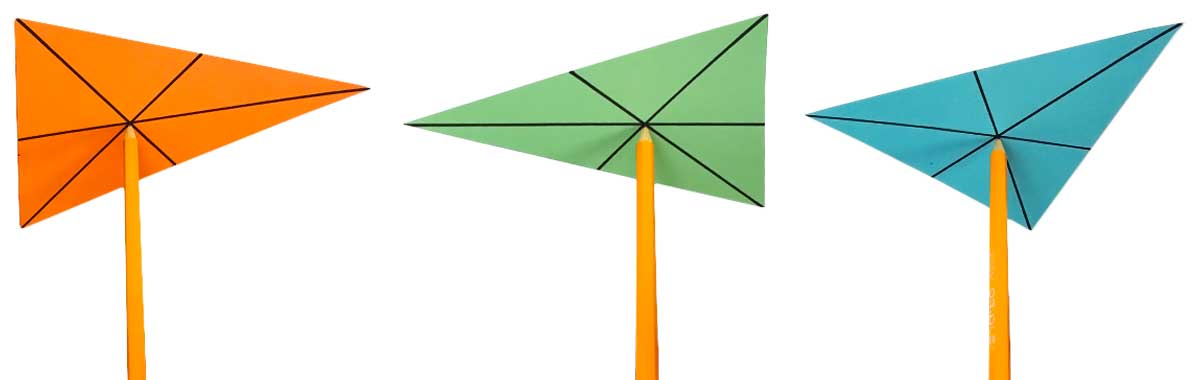
Bunun olmasının sebebi ağırlığın bu merkez etrafında dağılmış olmasıdır. Fizikte de bu noktaya ağırlık merkezi denmektedir.

Ağırlık merkezinden geçen bir doğru üçgeni alanları birbirlerine eşit olan iki parçaya ayırır. Sağdaki animasyonda mavi noktayı hareket ettirin. Kırmızı ve yeşil bölgelerin alanları birbirlerine eşit olacaktır.

Dik Doğru ve Çevrel Çember

Herhangi bir doğrunun ona dik doğrusu demek o doğru ile nda dik açı yapan doğru demektir.

Bu üçgenin kenarlara dik olan doğrusunu çiziniz. Kenara dik doğruyu çizmek için bir uç noktadan diğerine sürükleyerek bir doğru çiziniz.

Daha önce de olduğu gibi bu üç dik doğru bir noktada kesişiyorlar. Bu noktanın bir özelliği var.

Dik doğrunun üzerindeki bir noktaya dik doğrunun kesiştiği kenarın üzerindeki köşelerden çizilmiş iki doğrunun uzunlukları aynıdır. Örneğin, mavi dik doğru üzerindeki bir noktanın A ve C noktalarına uzaklıkları eşit. Kırmızı dik doğru üzerindeki bir noktanın noktalarına uzaklığı eşittir.

Kesişim noktası bütün dik doğruların üzerindedir. O zaman üçgenin olan uzaklıkları eşittir.

Bu demek oluyor ki bütün köşelere dokunan bir çember çizebiliriz. Bu çembere üçgenin çevrel çemberi diyoruz. Merkezi ise üç dik doğrunun kesişimi oluyor ve çevrel merkez diye adlandırılıyor.

Aslında, herhangi üç nokta verildiğinde bu üç noktanın orta noktalar olduğu bir üçgen çizilip daha sonra bu üç noktanın üzerinde olduğu kenarlara dik doğrular çizildikten sonra bu üç doğrunun kesişim noktasını merkez kabul eden ve üçgenin köşelerine değen bir çember çizilebilir. (Tabi eğer başta verilen üç nokta ise bu yapılabilir.)

Açı Ortaylar ve İç Teğet Çember

Muhtemelen şu an şuna takıldınız: bir yapı alıyoruz, kenarlara/açılara üç kez bir şeyler yapıyoruz ve daha sonra kesişimlerin ne gibi özellikleri var onlara bakıyoruz.

Bir açı iki ayrı eş parçaya bölen doğrulara açı ortay diyoruz. Yandaki üçgenin açı ortaylarını çiziniz. Bir açı ortay çizmek için açıların bulunduğu köşeler ile ortadaki nokta arasında bir çizgi çizmeniz gerekir.

Yeniden hatırlatalım, üç doğru tek bir noktada kesişir. Böyle bir şeyi doğal karşılıyoruz ama aslında bunun olması için elimizde geçerli bir sebep yok -- üçgenler yalnızca özel şekillerdir.

Açı ortayın üzerindeki herhangi bir noktanın, açıyı oluşturan iki kenara olan uzaklıkları eşittir. Örneğin, mavi doğrunun üzerindeki bir nokta a ve c kenarlarına eşit uzaklıkta bulunmakta. kırmızı doğrunun üzerindeki bir nokta kenarlarına eşit uzaklıkta bulunmakta.

Kesişim noktası bütün açı ortayların üzerindedir. Yani üçgenin üç olan uzaklıkları birbirlerine eşittir.

Yani bu kesişim noktası çevresinde kenarlara dokunan bir çember çizebiliriz. Bu çembere iç teğet çember, bu çemberin merkezine ise iç teğet merkezi diyoruz.

Alan ve Yükseklikler

Bir dikdörtgenin alanını bulmak kolay: yükseklik ve genişliği çarparak bulabiliyoruz. Bir üçgenin alanını bulmaksa nispeten daha zordur. Bir dikdörtgenin içine üçgen “yerleştirmek” ile başlayalım.

Dikdörtgenin genişliği üçgenin alt kenarı oluyor (taban diye adlandırılır.). Dikdörtgenin yüksekliği üçgenin tabanına karşısındaki köşeden uzatılmış dik yükseklik oluyor.

Yükseklik üçgeni iki parçaya ayırır. Yükseklik tarafından iki ayrılmış dikdörtgendeki üçgenden farklı alanların üçgendeki alanlar ile aynı olduğunu gözlemleyebiliriz.

Artık dikdörtgenin alanı ile uğraşabiliriz. Yani üçgenin alanı dikdörtgenin alanının yarısı olacak:

A=12× taban × yükseklik

Bir üçgenin alanını hesaplamak için herhangi bir kenarını taban olarak düşünüp o kenarın karşısındaki köşeden tabana yükseklik çizdikten sonra (bu yükseklik tabana ) yüksekliğin uzunluğu ile tabanın uzunluğunun çarpımının yarısını almak yeterli olacaktır.

Üçgenlerde bu yükseklikler genelde uzunluk diye adlandırılırlar. Bir üçgende üç tane vardır.

Tıpkı medyanlar, dik doğrular ve açı ortaylar konusunda olduğu gibi bu üç uzunluğun kesiştikleri bir nokta vardır. Bu noktaya yükseklik merkezi diyoruz.

Dar açılı üçgenlerde yükseklik merkezi üçgenin

Geniş açılı üçgenlerde yükseklik merkezi üçgenin

Dik açılı üçgenlerde yükseklik merkezi üçgenin İki uzunluk aslında üçgenin iki kenarıdır.

Dili değiştir

Mathigon'da oturum açın

Paylaş

İlerlemeyi Sıfırla

Sözlük

Üçgenler ve TrigonometriÜçgenlerin Özellikleri

Medyanlar

Dik Doğru ve Çevrel Çember

Açı Ortaylar ve İç Teğet Çember

Alan ve Yükseklikler