Bölünebilme ve AsallarAsalların Dağılımı
Bir sayının asal olup olmadığını kontrol etmenin en kolay yolu onu kendisinden küçük tüm tamsayılara bölmeye çalışmaktır. Bilgisayarlar bunu çok hızlı ve verimli bir şekilde yapabilir. Çok büyük sayılar, yüzlerce basamaklı, için daha verimli algoritmalar da vardır. Bunlardan bazıları bir sayının neredeyse kesinlikle asal olup olmadığını belirlemek için olasılığı kullanır.
İşte bir sayının asal olup olmadığını kontrol eden bir hesap makinesi:
Asal Kontrol Eder
${result}
Tarih boyunca insanlar büyük ve daha büyük asal sayıları bulmaya çalıştılar. 1460'ta, bilinen en büyük asal ayı 131,071'ti. 1772'te
Bilgisayarların da 20. yüzyılda gelişmesiyle büyük asal sayıları hesaplamak daha kolay hale geldi. Şu anda bilinen en büyük asal sayı Aralık 2018'de bulundu ve 24,862,048 basamaklı. Sayıyı yazmak için 800 sayfa kağıda ihtiyacımız var.

GIMPS (Great Internet Mersenne Prime Search) Mersenne asal sayılarını aramak için özgürce kullanılabilen bir yazılım kullanan gönüllülerin ortak bir projesidir.
Bu büyük asal sayıları hesaplamak zaman kaybı gibi görünebilir ancak daha sonra bu derste bilgisayarların büyük asal sayıları gerçek hayattaki çeşitli uygulamalarını öğreneceğiz.
Burada, girdiğiniz sayı kadar basamaklı kendi asal sayılarınızı oluşturabilirsiniz:
Here you can generate your own prime numbers with a given number of digits:
Asal Sayı Üretici
Basamak sayısı:
${result}
Ulam Spirali
Polonyalı matematikçi
Bütün tam sayıları 1'i ortaya yazacak şekilde dikdörtgen bir ızgaraya spiraller halinde dönerek yazıyoruz ve asal olanları vurguluyoruz.
Şu ana kadar Ulam Spirali çok heyecan verici görünmüyor. Eğer biraz uzaklaşırsak ilginç modeller ortaya çıkıyor. 160.000'e kadar olan asallar:
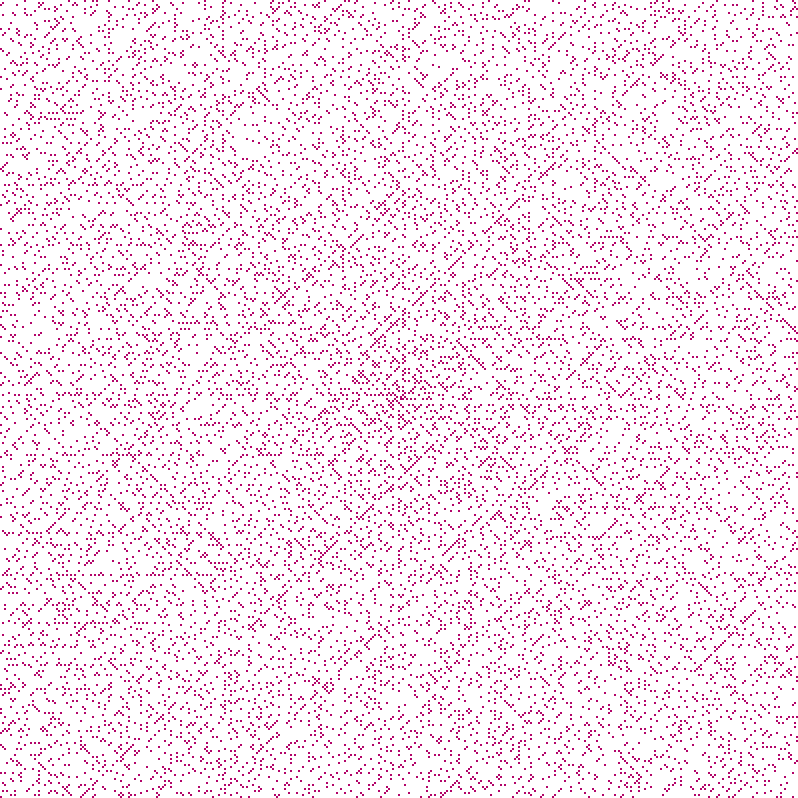
Rather than appearing randomly, as one might expect, it seems that certain diagonals are much more popular with primes than others. This creates a curious “plaid” pattern.
It turns out that these diagonals all correspond to certain quadratic equations which seem to generate prime numbers more often than average. However it is unknown why that would be the case…
Scientific American'ın Mart 1964 sayısının kapağı
Goldbach Sanısı
1742'de Alman matematikçi
Goldbach Hesap Makinesi
İki asal sayının toplamı olarak yazılmasını istediğiniz
herhangi bir çift tam sayı seçin.
${result}
Goldbach, gözlemini ünlü matematikçi
Bilgisayarlar Goldbach Sanısı'nın 4 × 1018'e kadar olan tüm çift sayılar için kontrol etti fakat matematikçiler hala her çift sayı için geçerli olan bir kanıt bulamadı. Bu ikisi çok farklı çünkü sonsuz sayıda tam sayı vardır ve hepsini kontrol edemeyiz.
Goldbach Sanısı'nın sadeliği, onu matematikteki çözülemeyen problemlerden en ünlülerinden biri haline getirdi.
İkiz Asallar
Asal sayıların büyüdükçe daha fazla yayıldığını görmüştük. Ama onlar her zaman tamamen rastgele olarak ortaya çıkıyorlar ve şans eseri iki tanesini yan yana buluyoruz: bunlara İkiz Asallar adını veriyoruz.
35,1113,4143,101103,20272029,108,377108,379,1,523,6511,523,653
Bilinen en büyük ikiz asal ikilisi tam 58.711 basamaklı! Sonsuz sayıda asal olduğu gibi sonsuz sayıda ikiz asal mı var? Kimse bilmiyor – İkiz Asal Sanısı da asal sayılar üzerine çözülmemiş problemlerden birisidir.
Riemann Hipotezi
Matematikçiler, asal sayılar arasındaki örüntüyü ve onların dağılımını araştırmak için yüzyıllar harcadılar. Asal sayılar tamamen rastgele görünmektedirler - bazen ardışık asallar arasında çok büyük boşluklar var ve bazen de
Alman matematikçi
When only 15 years old, the German mathematician
x ekseni boyunca tüm tam sayıları görebilirsiniz. Ne zaman bir asala rastlarsak Asal Sayan Fonksiyon (shown in blue) bir artıyor.
Ancak, yukarıda göreceğiniz gibi, asalların sayısı ve Gauss'un yakınsaması arasında hala önemli bir fark var. 1859'da,
Yüzlerce matematikçi Riemann'ın hipotezini kanıtlamaya çalıştı fakat hiçbiri başaramadı. Bu hipotezi genellikle en zor ve en önemli çözülemeyen problem olarak görülür. 2000'de, Clay Matematik Enstitüsü