English
عربى
中文
Deutsch
Español
Français
हिन्दी
Hrvatski
Italiano
日本語
Português
Română
Русский
Svenska
Türkçe
Tiếng ViệtÇokgenler ve ÇokyüzlülerPlatonik Katılar
Bu dersin başlangıcında, normal çokgen, tüm kenarların aynı uzunlukta ve tüm iç açıların aynı boyuta sahip olduğu bir çokgendir.
Normal bir polihedronda tüm Bir çokyüzlünün yüzleri, yüzeyini oluşturan çokgenlerdir. Bir çokyüzlünün "köşelerine" köşeleri denir. Bir Platonik katı, her yüzün aynı sayıda kenara sahip düzenli bir çokgen olduğu ve aynı sayıda yüzün her tepe noktasında buluştuğu bir çokyüzlülüktür. Sadece beş farklı Platonik katı vardır: Tetrahedron, Küp, Oktahedron, Dodecahedron ve Icosahedron. Platon_ (M.Ö. 425 – 347 ) antik Yunan’da bir filozoftu, - öğretmeni Socrates ve öğrencisi Aristoteles ile birlikte- Batı felsefesi ve biliminin temelini attı. Platon, Batı dünyasında ilk yüksek öğrenim kurumu olan Atina Akademisi'ni kurdu. Felsefe ve teoloji, bilim ve matematik, politika ve adalet üzerine yaptığı birçok yazı onu tüm zamanların en etkili düşünürlerinden biri yapar. Bir Platonik katı, her yüzün aynı sayıda kenara sahip düzenli bir çokgen olduğu ve aynı sayıda yüzün her tepe noktasında buluştuğu bir çokyüzlülüktür. Sadece beş farklı Platonik katı vardır: Tetrahedron, Küp, Oktahedron, Dodecahedron ve Icosahedron.
Peki Platonik katılar neye benziyor - ve kaç tanesi var? Üç boyutlu bir şekil yapmak için, her tepe noktasında buluşmak için en az
Her köşede üç eşkenar üçgen, üç tarafın da aynı uzunlukta olduğu bir üçgendir.
Dört eşkenar üçgen her tepe noktasında toplanırsa, farklı bir Platonik katı elde ederiz. Oktahedron denir ve
Her köşede
Her köşede
Ve her tepe noktasında yedi veya daha fazla üçgen de yeni polihedra üretmez: bir tepe noktasında o kadar çok üçgene sığacak kadar yer yoktur.
Bu, üçgenlerden oluşan
Her köşede
Her köşede
Sonra, düzenli beşgenleri deneyelim:
Her köşede
Daha önce olduğu gibi, dört veya daha fazla beşgen
Denenecek bir sonraki normal çokgen altıgenler:
Her köşede üç altıgen buluşuyorsa, hemen bir
Aynı şey altıdan fazla kenarı olan tüm normal çokgenler için de geçerlidir. Mozaik vermezler ve kesinlikle üç boyutlu çokgenler almayız.
Bu, sadece
dört yüzlü şekil
Küp
sekizyüzlü
oniki yüzlü şekil
ikosahedron
Yüzlerin ve köşelerin sayısının nasıl HER ŞEY
Her yüzünü bir tepe noktasıyla ve her tepe noktasını bir yüzle “değiştirerek” bir çokyüzlüyü ikili haline getirebiliriz. Bu animasyonlar nasıl olduğunu gösterir:
Tetrahedron kendisiyle ikili. Aynı sayıda yüze ve köşeye sahip olduğundan, onları değiştirmek hiçbir şeyi değiştirmez.
Platon_ (M.Ö. 425 – 347 ) antik Yunan’da bir filozoftu, - öğretmeni Socrates ve öğrencisi Aristoteles ile birlikte- Batı felsefesi ve biliminin temelini attı. Platon, Batı dünyasında ilk yüksek öğrenim kurumu olan Atina Akademisi'ni kurdu. Felsefe ve teoloji, bilim ve matematik, politika ve adalet üzerine yaptığı birçok yazı onu tüm zamanların en etkili düşünürlerinden biri yapar.
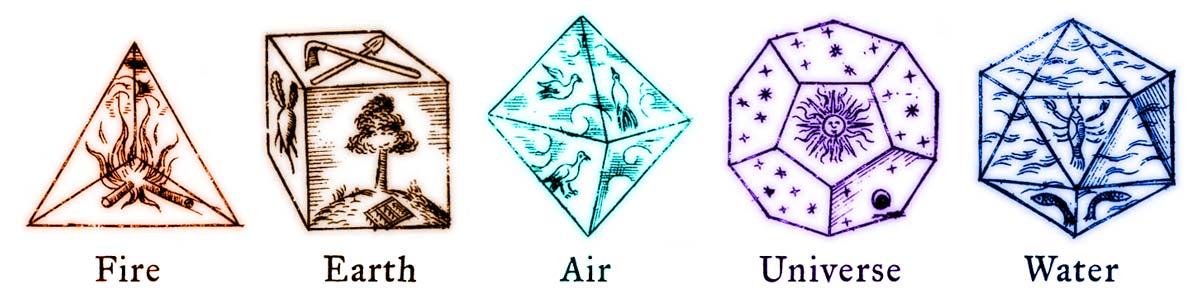
Images from Johannes Kepler’s book “Harmonices Mundi” (1619)
Arşimet Katıları
Platonik katılar özellikle önemli polihedradır, ancak sayısız başkaları da vardır.
Örneğin Bir Arşimet katı, her yönden aynı görünen farklı normal çokgen türlerinden oluşan bir çokyüzlülüktür. 13 farklı Arşimet katı vardır. normal çokgen, tüm kenarların aynı uzunlukta ve tüm iç açıların aynı boyuta sahip olduğu bir çokgendir. Arşimed (M.Ö. 287 – 212 ) eski bir Yunan bilim insanı ve mühendisiydi. Tüm zamanların en büyük matematikçilerinden biriydi. Birçok matematik kavramını keşfetti. Geometri, analiz ve mekanik alanlarında çalıştı. Arşimed, banyo yaparken, cisimlerin suya batırılımasıyla meydana gelen suyun yer değiştirme miktarını kullanarak düzensiz cisimlerin hacmini belirlemenin bir yolunu buldu. Bu keşif sayesinde öylesine heyecanlandı ki, sokakta, hala soyunmuş halde iken “Eureka!” diye bağırdı (Yunanca’da “Onu buldum!”). Sicilya'daki memleketi Syracuse'nin kuşatması sırasında, bir mühendis olarak, ustalıkla savunma makineleri yaptı. İki yıl sonra, Romalıların sonunda girmeyi başardığı Syracuse’ta Arşimed öldürüldü. Son sözleri, o sırada üzerinde çalıştığı “Çemberlerime dokunma” idi.
Kesik Tetrahedron 8 yüz, 12 köşe, 18 kenar
Cuboctahedron 14 yüz, 12 köşe, 24 kenar
Kesik Küp 14 yüz, 24 köşe, 36 kenar
Kesik Oktahedron 14 yüz, 24 köşe, 36 kenar
Rhombicuboctahedron 26 yüz, 24 köşe, 48 kenar
Kesik Cuboctahedron 26 yüz, 48 köşe, 72 kenar
Snub Cube 38 yüz, 24 köşe, 60 kenar
Icosidodecahedron 32 yüz, 30 köşe, 60 kenar
Kesik Dodecahedron 32 yüz, 60 köşe, 90 kenar
Kesik İkosahedron 32 yüz, 60 köşe, 90 kenar
Rhombicosidodecahedron 62 yüz, 60 köşe, 120 kenar
Kesik İkosidodekahedron 62 yüz, 120 köşe, 180 kenar
Snub Dodecahedron 92 yüz, 60 köşe, 150 kenar
Uygulamalar
Platon, tüm elementlerin Platonik katılardan oluştuğuna inanmakta yanlıştı. Ancak düzenli polihedra, doğada başka yerlerde görünmelerini sağlayan birçok özel özelliğe sahiptir - ve bu özellikleri bilim ve mühendislikte kopyalayabiliriz.
Radiolaria skeleton
Icosahedral virus
Birçok virüs , bakteri ve diğer küçük organizmalar Icosahedron, bir Platonik katıdır ve hepsi eşkenar üçgen olan 20 yüzden oluşur. 12 köşesi ve 30 kenarı vardır.
Buckyball molecule
Montreal Biosphere
Birçok molekül düzenli polihedra şeklindedir. Bunun en ünlü örneği Kesik İkosahedron, 12 düzenli beşgen ve 20 düzenli altıgen içeren bir _Arşimet katıdır.
Bilim adamları yıldızlararası tozu araştırdıkları 1985 yılında keşfedildi. Benzer görünüşlü binalar inşa etmesiyle ünlü mimar Richard Buckminster “Bucky” Fuller (1895 – 1983) Amerikalı bir mimar, tasarımcı ve mucittir. Kocaman, küresel yapılar olan jeodezik kubbeler inşalarıyla ünlüdür. Benzer görünümdeki karbon molekülü _fullerenes_in adı buradan gelir.
Fluorite octahedron
Pyrite cube
Çoğu kristal atomlarını Tetrahedron bir Platonik katıdır ve eşkenar üçgen olan dört yüzden oluşur. Dört köşesi ve altı kenarı vardır. Bir küp (bazen Hexahedron olarak adlandırılır), her yüzün kare olduğu normal bir çokyüzlüdür. Beş Platonik katıktan biridir ve 6 yüzü, 8 köşesi ve 12 kenarı vardır. Oktahedron bir Platonik katıdır ve eşkenar üçgen olan 8 yüzden oluşur. 6 köşesi ve 12 kenarı vardır.
Octagonal space frames
Louvre museum in Paris
Tetrahedra ve oktahedra inanılmaz derecede sert ve kararlıdır, bu da onları inşaatta çok yararlı kılar. Uzay çerçeveleri , büyük çatıları ve ağır köprüleri destekleyebilen çokgen yapılardır.
Football
Polygonal role-playing dice
Platonik katılar da zar oluşturmak için kullanılır. simetrileri nedeniyle, her iki tarafın yukarı bakma olasılığı, 0 ile 1 arasında, belirli bir olayın gerçekleşme olasılığını gösteren sayıdır. Bir olayın olasılığı A
Kesik İkosahedron, 12 düzenli beşgen ve 20 düzenli altıgen içeren bir _Arşimet katıdır.