Çokgenler ve ÇokyüzlülerTessellations

Çokgenler doğanın her yerinde görülür. Geniş bir alanı döşemek istiyorsanız özellikle kullanışlıdır, çünkü çokgenleri boşluk veya çakışma olmadan birbirine sığdırabilirsiniz. Bunun gibi desenlere mozaikleme denir.

İnsanlar antik Roma'dan günümüze sanat, mimari ve teknolojideki bu doğal modellerin çoğunu kopyaladılar. İşte birkaç örnek:

Burada düzenli çokgenler kullanarak kendi mozaiklerinizi oluşturabilirsiniz. Yeni şekilleri kenar çubuğundan tuvale sürüklemeniz yeterlidir. Hangi şekiller iyi mozaik oluşturur? Hiç mozaik oluşturmayan şekiller var mı? İlginç desenler yaratmaya çalışın!

Examples of other students’ tessellations

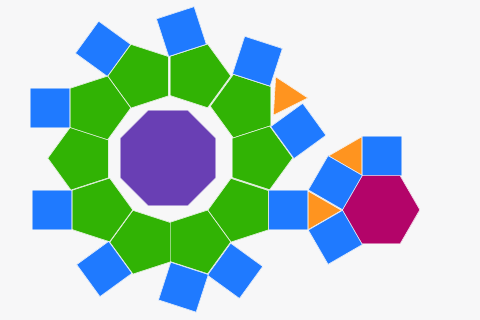
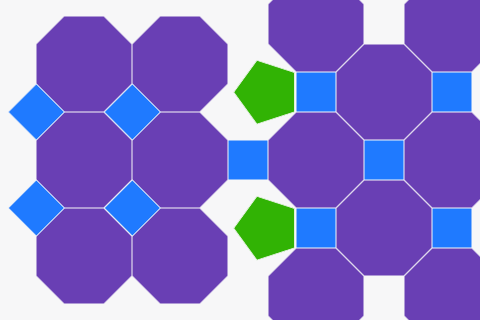
Normal çokgenlerden mozaikler

Bazı düzenli çokgenlerin ( gibi) beşgenler ) kolayca döşenirken, diğerleri ( gibi) üçgenler altıgenler ) hiç mozaik görünmüyor.

Bu, daha önce hesaplamayı öğrendiğimiz iç açılarının büyüklüğü ile ilgilidir. Mozaikleme işleminin her köşesinde , birden çok farklı çokgenin iç açıları birleşir. ° 'ye kadar eklemek için tüm bu açılara ihtiyacımız var, aksi takdirde bir boşluk veya bir çakışma olacaktır.

Benzer şekilde, tıpkı beşgenler gibi, 7 veya daha fazla kenarı olan herhangi bir normal çokgenin mozaik oluşturmadığını kontrol edebilirsiniz. Bu, mozaikleyen tek normal çokgenlerin üçgenler, kareler ve altıgenler olduğu anlamına gelir!

Tabii ki, iç açılarının 360° 'ye kadar çıkabilmesi şartıyla, farklı türde düzenli çokgenleri mozaik içinde birleştirebilirsiniz:

Squares and triangles
90° + 90° + 60° + 60° + 60° = 360°

Squares and triangles
90° + 90° + 60° + 60° + 60° = 360°

Hexagons and triangles
120° + 120° + 60° + 60° = 360°

Hexagons and triangles
120° + 60° + 60° + 60° + 60° = 360°

Hexagons, squares and triangles
120° + 90° + 90° + 60° = 360°

Octagons and squares
135° + 135° + 90° = 360°

Dodecagons (12-gons) and triangles
150° + 150° + 60° = 360°

Dodecagons, hexagons and squares
150° + 120° + 90° = 360°

Düzensiz poligonlardan mozaikler

Ayrıca, döndürürken ve düzenlerken dikkatli olduğumuz sürece düzensiz çokgenlerden mozaikler yapmayı deneyebiliriz.

Beşgenler biraz daha hileli. Normal beşgenlerin zaten gördük tessellate , ama normal olmayanlar ne olacak?

İşte beşgenlerle üç farklı mozaik örneği. Normal değildirler, ancak mükemmel şekilde geçerli 5 taraflı çokgenlerdir.

Şimdiye kadar, matematikçiler (dışbükey) beşgenlerle sadece 15 farklı mozaik türü buldular - en sonuncusu 2015 yılında keşfedildi. Kimse başka olup olmadığını bilmiyor ya da bu 15'in tek olup olmadığını bilmiyor…

Sanatta Mozaikler

Mozaikler biz birçok sanatçı, mimar ve tasarımcı - en ünlü Hollandalı sanatçı MC Escher için bir araç ve ilham kaynağı. Escher'ın çalışması garip, mutasyona uğramış yaratıklar, desenler ve manzaralar içeriyor:

Bu sanat eserleri genellikle eğlenceli ve zahmetsiz görünür, ancak altta yatan matematik ilkeleri öncekilerle aynıdır: açılar, rotasyonlar, çeviriler ve çokgenler. Matematik doğru değilse mozaikleme işe yaramaz!

“Metamorphosis II” by M. C. Escher (1940)

Penrose Tilings

Şimdiye kadar gördüğümüz tüm mozaiklerin ortak bir yanı var: bunlar periyodik . Bu, tekrar tekrar tekrarlanan düzenli bir kalıptan oluştuğu anlamına gelir. Sonsuza kadar her yöne devam edebilirler ve her yerde aynı görünürler.

1970'lerde İngiliz matematikçi ve fizikçi Roger Penrose periyodik olmayan mozaikleri keşfetti - hala her yönden sonsuzca devam ediyorlar, ama asla aynı görünmüyorlar. Bunlara Penrose eğimleri denir ve bir tane oluşturmak için sadece birkaç farklı çokgen türüne ihtiyacınız vardır:

Penrose, mozaikleri sadece eğlence için araştırıyordu, ancak bazı gerçek malzemelerin (alüminyum gibi) iç yapısının benzer bir desen izlediği ortaya çıktı. Desen tuvalet kağıdında bile kullanıldı, çünkü üreticiler periyodik olmayan bir desenin herhangi bir çıkıntı olmadan toplanabileceğini fark ettiler.