Dönüşümler ve SimetriSimetri Grupları ve Duvarkağıdı Grupları
Bazı şekiller birden fazla simetriye sahiptir – basit bir örnek olarak








Yukarıda karenin
Ayrıca
Ve son olarak, “hiçbir şey yapmamayı” başka bir özel simetri çeşidi olarak düşünebiliriz – çünkü sonuç, öncekiyle (açıkça) aynı olacak. Bu bazen etkisiz eleman olarak adlandırılır.
Toplamda,
Şimdi bu simetrilerle biraz aritmetik yapmaya başlayabiliriz. Örneğin, yeni bir simetri elde etmek için iki simetriyi toplayabiliriz.






Karenin iki simetrisini topladığınız zaman yeni bir tanesine ulaşırsınız. İşte kendiniz deneyebilmeniz için “simetri hesap makinesi”:
Simetri hesap makinesiyle biraz zaman harcayın ve her bir yönlendirmeyi bulmayı deneyin. Bu gözlemleri tamamlayabilir misiniz?
- İki döndürmeyi topladığınızda daima
(veya etkisiz eleman). - İki yansımayı topladığınızda daima
(veya etkisiz eleman). - Aynı iki simetriyi ters sırayla topladığınızda
verir. - Etkisiz elemanını eklemek
.
Daha önce simetrileri toplamanın aslında tam sayıları toplamaya benzediğini fark etmiş olabilirsiniz:
- simetrileri/tam sayıları toplamak daima başka bir simetri/tam sayı verir:
+ = 12 + 7 = 19 - simetrileri/tam sayıları toplama işlemi
birleşme özelliğine sahiptir:+ + = + + 4 + 2 + 5 = 4 + 2 + 5 - Her simetrinin/tam sayının , simetri/tam sayı olan bir tersi vardır ve toplandıklarında etkisiz elemanı verir:
+ = 4 + –4 = 0
Matematikte, bu özelliklere sahip her koleksiyon
Bu örnekte, karenin sekiz simetrisiyle başladık. Aslında, her geometrik şekil kendi simetri grubuna sahiptir. Hepsinin farklı elemanları vardır fakat daima yukarıdaki üç kuralı sağlarlar.
Gruplar matematikte her zaman karşımıza çıkar. Elemanlar sayılar ya da simetriler olabilir, veya polinomlar, permütasyonlar, matrisler, fonksiyonlar… üç kuralı sağlayan herhangi bir şey olabilir. Grup Teori’nin kilit noktası tek tek elemanlarla değil elemanların birbirlerini nasıl etkiledikleriyle ilgilenmektir.
Örneğin, farklı moleküllerin simetri grubu bilim insanlarına ilgili materyallerin özelliklerini tahmin etme ve açıklama konusunda yardımcı olabilir.
Gruplar tahta oyunlarını kazanma stratejisinin, virüslerin davranışlarının, müzikteki farklı harmonilerin analizinde ve başka birçok alanda da kullanılır...
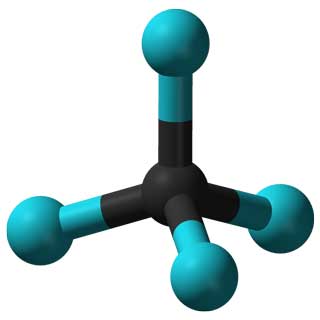
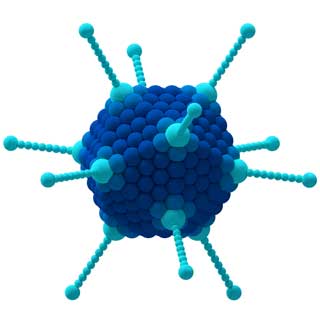
CCl4 molekülünün özellikleri (solda) ve Adenovirüs (sağda) simetrileriyle belirlenmiştir.
Duvarkağıdı Grupları
Önceki bölümlerde iki çeşit simetriyi ele aldık, bunlar iki farklı dönüşüme karşılık geliyordu: Döndürme ve yansıtma. Ancak üçüncü bir simetri türü daha var, bu da üçüncü çeşit bir dönüşüme karşılık gelir:


Altıgen bal peteği


Seramik duvar kaplaması
Yansıtma, döndürme ve öteleme simetrilerinin dışında dördüncü bir simetri çeşidi bile vardır::


Bir örüntü birden fazla simetri çeşidine sahip olabilir. Ve aynen kare için yaptığımız gibi, bir örüntünün de
Böyle gruplar bir örüntünün nasıl göründüğü(örneğin renkleri ve şekilleri) hakkında pek bir şey söylemez, sadece nasıl tekrar ettiğini söyler. Birden çok örüntü aynı simetri grubuna sahip olabilir, yalnızca aynı şekilde dizilip tekrar etmeleri yeterlidir.


Simetriler renklerle ya da yüzeysel şekillerle ilgili değildir. Farklı görüntülerine rağmen bu iki örüntü aynı simetrilere sahiptir.


Bu iki örüntü, birbirlerinden çok soldaki örüntülere benzemelerine rağmen, aslında aynı simetrilere sahiptirler.
Sonsuz farklı örüntü düşünebilmemize rağmen, aslında toplamda sadece 17 tane simetri grubu olduğu keşfedildi. Bunlara Duvarkağıdı Grupları diyoruz. Her duvarkağıdı grubu öteleme, döndürme, yansıtma ve kaydırarak yansıtmaların bir kombinasyonu ile tanımlanır. Bu örneklerdeki

P1 tipi
Sadece ötelemeler

P2 tipi
2 dereceli döndürmeler, ötelemeler

P3 tipi
2 dereceli(180°) dört döndürme, ötelemeler

P4 tipi
3 dereceli(120°) döndürmeler, ötelemeler

P6 tipi
2, 3 ve 6(60°) dereceli döndürmeler, ötelemeler

PM tipi
Paralel yansıtma eksenleri, ötelemeler

PMM tipi
Dik yansımalar, 2 dereceli döndürmeler, ötelemeler

P4M tipi
(2 + 4 dereceli) Döndürmeler, yansımalar, kaydırıp yansımalar, ötelemeler

P6M tipi
(2 + 6 dereceli) Döndürmeler, yansımalar, kaydırıp yansımalar, ötelemeler

P3M1 tipi
3 dereceli döndürmeler, yansımalar, kaydırıp yansımalar, ötelemeler

P31M tipi
3 dereceli döndürmeler, yansımalar, kaydırıp yansımalar, ötelemeler

P4G tipi
(2 + 4 dereceli) Döndürmeler, yansımalar, kaydırıp yansımalar, ötelemeler

CMM tipi
Dik yansıtmalar, 2 dereceli döndürmeler, ötelemeler

PMG tipi
Yansımalar, kaydırıp yansıtmalar, 2 dereceli döndürmeler, ötelemeler

PG tipi
Paralel kaydırıp yansıtmalar, ötelemeler

CM tipi
Yansımalar, kaydırıp yansıtmalar, ötelemeler

PGG tipi
Dik kaydırıp yansıtmalar, 2 dereceli döndürmeler, ötelemeler
Maalesef bu gruplardan neden 17 tane olduğunun basit bir açıklaması yok. Bunun kanıtlanması da çok daha ileri seviyede matematik gerektiriyor...
Onun yerine, 17 duvarkağıdı grubuna karşılık gelen kendi örüntülerinizi çizmeyi deneyebilirsiniz.
Examples of other students’ drawings



Duvarkağıdı grupları düzlemsel, iki boyutlu örüntüler ile ilgiliydi. Üç boyut için de benzer bir şey yapabiliriz: böyle gruplara kristal grupları denir, ve 219 tane kristal grubu var!
Kristal grupları öteleme, yansıtma, döndürme ve kaydırıp yansıtmaya ek olarak kaydırma düzlemleri ve burgu eksenleri(şişe kapağını açarkenki hareketinizi düşünün) gibi simetriler de içerirler.
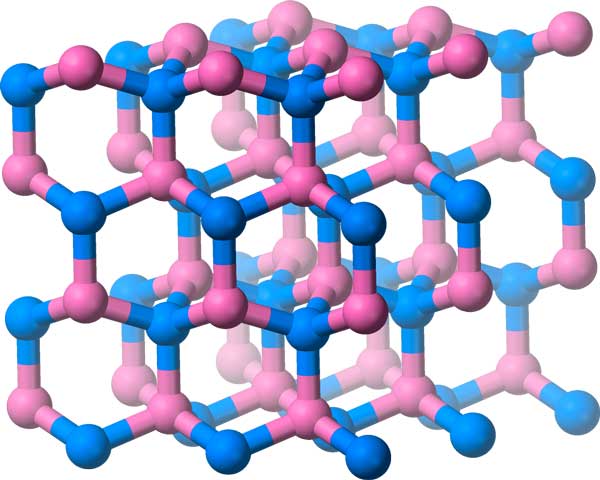
Boron-Nitrat molekülleri kristal kafes şeklinde dizilmiştir ve kendisi 3 boyutlu simetri grubuna sahiptir.